Reed-Solomon Fingerprinting
Articles based on Justin Thaler's Proofs, Arguments, and Zero-Knowledge
Justin Thaler’s book Proofs, Arguments, and Zero-Knowledge is an excellent monograph on verifiable computing. This article is part of a series that will paraphrase and distill key sections of the book from the perspective of a protocol engineer.
We begin with chapter 2 as this is where the book itself begins technical analysis of proving systems.
Reed-Solomon Fingerprinting
Chapter 2 of Thaler’s book is entitled The Power of Randomness. It explores how a probabilistic procedure can be used to maximize the efficiency of communication required to verify equality of some data held by two independent parties. These parties are, naturally, called Alice and Bob.
Alice and Bob want to verify that they possess the same ASCII encoded file. The file could be very large. Its size in characters is denoted by n.
No deterministic procedure can be used to communicate less information than the trivial solution of sending Alice’s file to Bob. However, a randomized procedure can be used to reduce communication cost exponentially; so long as this procedure has negligible probability of producing an incorrect result.
One such such procedure involves creating a short “fingerprint” of Alice’s file. This fingerprint approximates a unique identifier to a sufficiently high degree. In order to produce the fingerprint, we use a hash function.1
For the purposes of the hash function, we select a prime number, p, greater than n².2 This is because we want all arithmetic to be done in a finite field, Fp, which can represent at least as many integers as there are elements in the input’s domain. Our input is Alice’s ASCII encoded file, so the input domain has 128 elements:
Whereas the finite field has at least 128² elements:
Alice selects a random field element, x, from this finite field:
The hash function interprets its input as the coefficients of a univariate polynomial of degree n-1, and outputs the polynomial evaluated at x.3 The polynomial represents a Reed-Solomon encoding of the input vector. Ultimately we want to evaluate this polynomial so that we can send the result to Bob:
If you prefer to think in code, you can take a look at my rough implementation of this here. It involves a fair bit of boilerplate for the FieldElement type and its arithmetic operations so here is a snippet of the most relevant parts:
fn hash(a: &[FieldElement], x: FieldElement) -> FieldElement {
a.iter()
.enumerate()
.fold(FieldElement::new(0, x.modulus), |y, (i, &a)| {
y + a * x.pow(i as u64)
})
}
fn main() {
let n = 128u64;
let p = n.pow(2);
let a: Vec<FieldElement> = (1..=n).map(|a| {
FieldElement::new(a, p)
}).collect();
let x = FieldElement::new(511, p);
let y = hash(&a, x);
println!("h(a, x={x}, p={p}) = {y}");
}The communication protocol is that Alice picks a random element x from the finite field, executes the above-defined hash function on the series of ASCII characters and sends Bob the output, y, along with x. Bob executes the same hash function with x and his file and compares his output to that of Alice’s.
If Bob’s y matches Alice’s, Bob resolves that the results would be equal for every possible choice of x. This is a deterministic corollary based on the nature of the hash function’s equation we mentioned above - if all coefficients match, it doesn’t matter which field element you specify for x. However, to understand why Bob can conclude that the files are not equal on the basis of unequal y values, we need to understand the probabilities at play.
Two unequal polynomials of degree at most n, with coefficients in some finite field Fp, can evaluate to the same field element from the same input for at most n values in Fp.4 So the probability that Alice picks an x which evaluates to the same y for two unequal polynomials is (n-1)/p. If p is sufficiently large, then the chance of this happening is negligible.
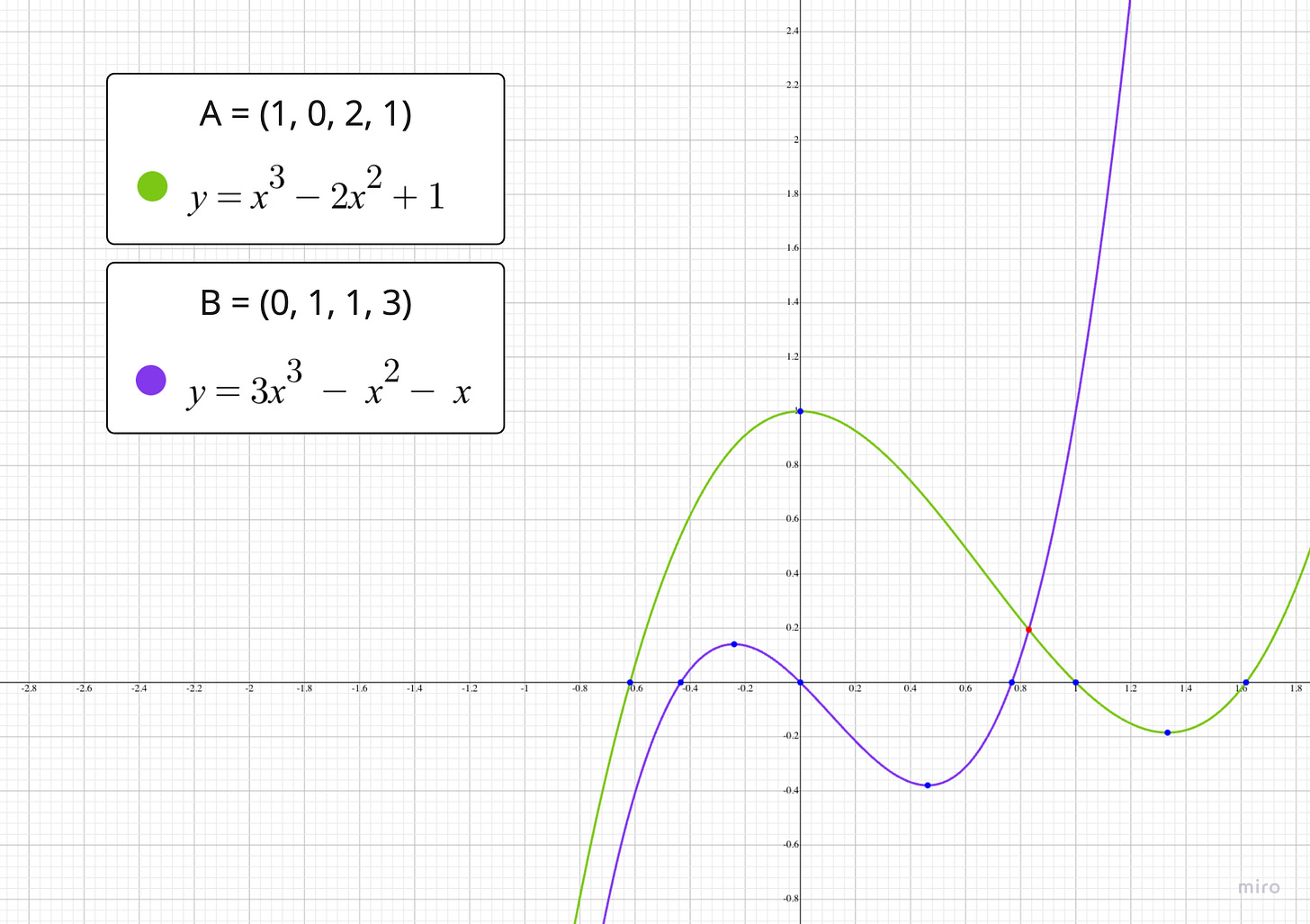
We can visualize this low probability with a simple example. Lets take a look at a representation of two small vectors as polynomials over real numbers.5 Each vector contains only four elements so their corresponding polynomials are of degree 3 at most.
Observe that the polynomials only share one equal evaluation for x. But there are many more unequal evaluations. The same is true for our protocol where we use polynomials over a finite field. The number of unequal valuations depends on the finite field because it determines the size of our domain. The larger the p compared to the degree of the polynomials, the greater the disparity between equal and unequal evaluations grows. This is why we chose p to be at least n² earlier.
So when Bob observes a discrepancy between his output and that of Alice’s, he knows that Alice could not have selected an x which evaluates to the same y across two unequal polynomials. The chance that Bob’s conclusion is correct is 1-(n-1)/p. And because we specified that p>=n² we know that this is at least 1-1/n.
Because the protocol only involves communication of two field elements (x and y), we are able to achieve an exponential improvement in communcation over the deterministic approach.
To conclude, we saw that there is a relationship between the finite field’s order, p, and the length of the input, n which affects the probabilities relied on by our protocol. We also saw that the input domain (128 ASCII characters) is treated as a subset of the finite field; meaning the procedure involves an extension of the input domain.
Now we can start to understand how we can use polynomials over finite fields to provide probabilistic solutions to problems that would otherwise require impractical, deterministic approaches.
In the next article we will explore the remainder of chapter 2 which constructs more sophisticated probabilistic procedures through Freivald’s algorithm and Lagrange interpolation.
A cryptographic hash function is not used in this section for the purposes of the communication protocol.
This assumes that the square of the length of the file is greater than the number of unique characters in ASCII (128).
x is the monomial in the univariate polynomial.
This is Fact 2.1 from the book. Later, it is revealed that fact 2.1 is a special (univariate) case of the Schwartz-Zippel Lemma.